Mark the correct alternative in the following:

Which of the following is not correct?

We are given that,

A = [a_ij]_3×3

That is, order of matrix A = 3

Example:

Let,

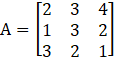
Take determinant of A.

Determinant of 3 × 3 matrices is found as,

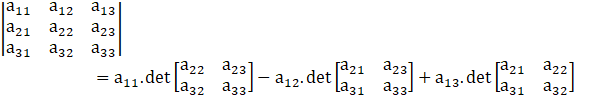
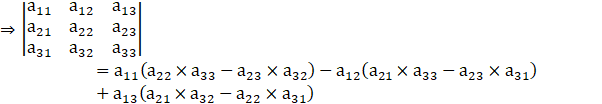
So,

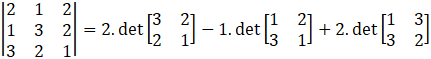
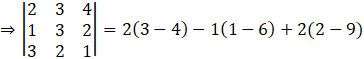
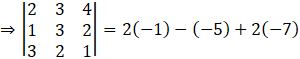
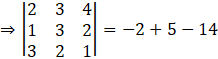
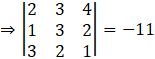
⇒ |A| = -11

The transpose of a matrix is a new matrix whose rows are the columns of the original.

So,

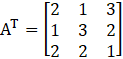
Determinant of A^T:

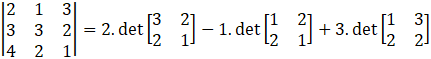
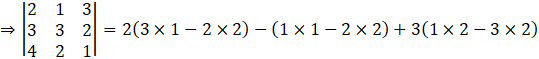
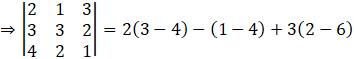
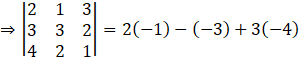
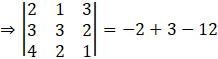
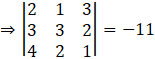
So, we can conclude that,

|A| = |A^T|, where A = [a_ij]_3×3.

Option (B) is correct.

|kA| = k³|A|, where A = [a_ij]_3×3

Example:

Let k = 2.

And,

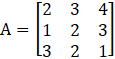
Take Left Hand Side of the equation:

LHS = |kA|

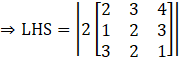
Multiply 2 by each term of the matrix.

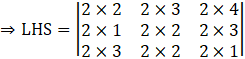
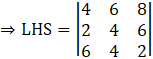
⇒ LHS = 4(4 × 2 – 6 × 4) – 6(2 × 2 – 6 × 6) + 8(2 × 4 – 4 × 6)

⇒ LHS = 4(8 – 24) – 6(4 – 36) + 8(8 – 24)

⇒ LHS = 4(-16) – 6(-32) + 8(-16)

⇒ LHS = -64 + 192 – 128

⇒ LHS = 0

Take Right Hand Side of the equation:

RHS = k³|A|

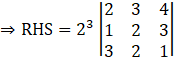
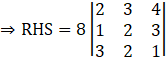
⇒ RHS = 8 [2(2 × 1 – 3 × 2) – 3(1 × 1 – 3 × 3) + 4(1 × 2 – 2 × 3)]

⇒ RHS = 8 [2(2 – 6) – 3(1 – 9) + 4(2 – 6)]

⇒ RHS = 8 [2(-4) – 3(-8) + 4(-4)]

⇒ RHS = 8 [-8 + 24 – 16]

⇒ RHS = 8 × 0

⇒ RHS = 0

Since, LHS = RHS.

We can conclude that,

|kA| = k³|A|, where A = [a_ij]_3×3

Option (C) is also correct.

If A is a skew-symmetric matrix of odd order, then |A| = 0.

If the transpose of a matrix is equal to the negative of itself, the matrix is said to be skew symmetric. In other words, A^T = -A.

Example,

Let a matrix of odd order 3 × 3 be,

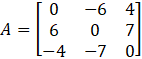
Take determinant of A.

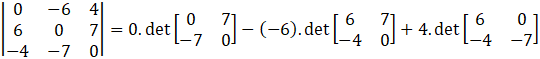
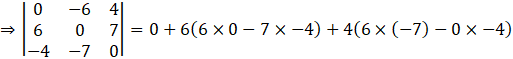
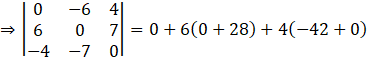
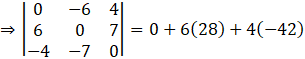
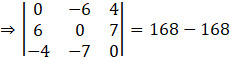
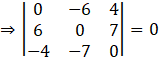
Thus, we can conclude that

If A is a skew-symmetric matrix of odd order, then |A| = 0.

Option (D) is incorrect.

Let a = 1, b = 3, c = 3, d = -4, e = -2, f = 5, g = 0 and h = 2.

Take Left Hand Side,

⇒ LHS = 4 × 2 – (-1) × 3

⇒ LHS = 8 + 3

⇒ LHS = 11

Take Right Hand Side,

⇒ RHS = (1 × 0 – 3 × (-2)) + (3 × 2 – (-4) × 5)

⇒ RHS = (0 + 6) + (6 + 20)

⇒ RHS = 6 + 26

⇒ RHS = 32

Since, LHS ≠ RHS. Then, we can conclude that,