Mark the correct alternative in the following:

If , then

We are given that,

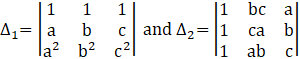
Let us find the determinants ∆₁ and ∆₂.

We know that,

Determinant of 3 × 3 matrix is given as,

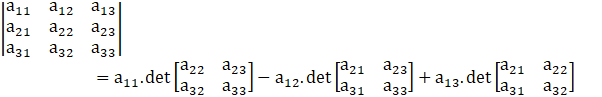
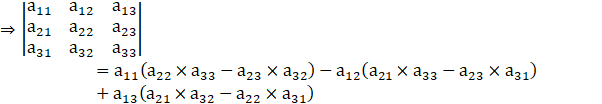
So,

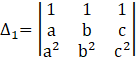
⇒ ∆₁ = (b × c² – c × b²) – (a × c² – c × a²) + (a × b² – b × a²)

⇒ ∆₁ = bc² – b²c – ac² + a²c + ab² – a²b …(i)

Also,

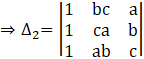
⇒ ∆₂ = (ca × c – b × ab) – bc(1 × c – b × 1) + a(1 × ab – ca × 1)

⇒ ∆₂ = ac² – ab² – bc(c – b) + a(ab – ac)

⇒ ∆₂ = ac² – ab² – bc² + b²c + a²b – a²c …(ii)

Checking Option (A).

Adding ∆₁ and ∆₂ by using values from (i) and (ii),

∆₁ + ∆₂ = (bc² – b²c – ac² + a²c + ab² – a²b) + (ac² – ab² – bc² + b²c + a²b – a²c)

⇒ ∆₁ + ∆₂ = bc² – bc² – b²c + b²c – ac² + ac² + ab² – ab² – a²b + a²b

⇒ ∆₁ + ∆₂ = 0

Thus, option (A) is correct.

Checking Option (B).

Multiplying 2 by (ii),

2∆₂ = 2(ac² – ab² – bc² + b²c + a²b – a²c)

⇒ 2∆₂ = 2ac² – 2ab² – 2bc² + 2b²c + 2a²b – 2a²c …(iii)

Then, adding 2∆₂ with ∆₁,

∆₁ + 2∆₂ = (bc² – b²c – ac² + a²c + ab² – a²b) + (2ac² – 2ab² – 2bc² + 2b²c + 2a²b – 2a²c)

⇒ ∆₁ + 2∆₂ = bc² – 2bc² – b²c + 2b²c – ac² + 2ac² + ab² – 2ab² – a²b + 2a²b

⇒ ∆₁ + 2∆₂ = -bc² + b²c + ac² – ab² + a²b

⇒ ∆₁ + 2∆₂ ≠ 0

Thus, option (B) is not correct.

Checking option (C).

Obviously, ∆₁ ≠ ∆₂

Since, by (i) and (ii), we can notice ∆₁ and ∆₂ have different values.

Thus, option (C) is not correct.