Choose the correct answer. Let f(x) = (x + |x|) |x|. Then, for all x

Question

Philoid · Accepted Answer

Given that f(x) = (x + |x|) |x|

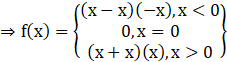
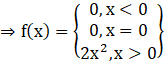
So, we can say that f(x) is continuous for all x.

Now, checking the differentiability at x =0

LHD at x =0,

RHD at x =0,

∵ LHD = RHD

So, f(x) is differentiable for all x.

Hence, option A is correct.

Choose the correct answer.Let f(x) = (x + |x|) |x|. Then, for all x