If ![]() are the position vectors of the vertices of a triangle, then write the position vector of its centroid.
are the position vectors of the vertices of a triangle, then write the position vector of its centroid.
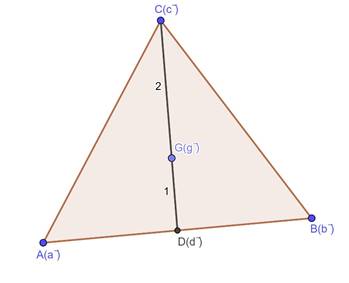
In the figure, D is the mid-point of AB, so it divides AB in 1:1 ratio. CD is a median of ∆ABC. G is the centroid of the triangle and by the property of triangle, G divides CD in 2:1 ratio.
The position vector of point D can be calculated using the section formula for vector, which states that the position vector of a point(![]() ) dividing two position vectors(
) dividing two position vectors(![]() ) in ration m:n, internally is
) in ration m:n, internally is
![]()
So, ![]()
Similarly, using section formula for G between points C and D, we get
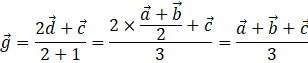
1