Show that the diagonals of a rhombus divide it into four congruent triangles.

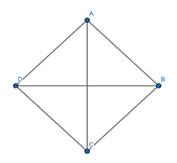
Given :- ABCD is a rhombus

Formula used :-

*SSS congruency rule

If all sides of both triangles are equal then both triangles are congruent

*properties of rhombus

Solution :-

In Δ AOD and Δ COB

AO=OC [diagonal of Rhombus bisect each other]

OD=OB [diagonal of Rhombus bisect each other]

AD=BC [all sides of rhombus are equal]

∴ Δ AOD ≅ Δ COB

In Δ AOB and Δ COD

AO=OC [diagonal of Rhombus bisect each other]

OD=OB [diagonal of Rhombus bisect each other]

CD=BA [all sides of rhombus are equal]

∴ Δ AOB ≅ Δ COD

In Δ AOB and Δ AOD

AO=AO [Common in both triangles]

OD=OB [diagonal of Rhombus bisect each other]

AD=AB [all sides of rhombus are equal]

∴ Δ AOB ≅ Δ AOD

∴ All four triangles divide by diagonals of triangle are congruent