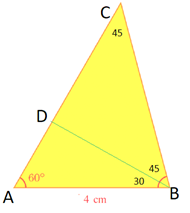
Calculate the perimeter and area of the triangle in the picture.

We name the vertices of the triangle as A, B and C. We draw a perpendicular from B on AC as BD.

In ΔABD,

⇒ ∠A + ∠ABD + ∠ADB = 180° (Sum of all angles of a triangle)

⇒ 60 + ∠ABD + 90 = 180°

⇒ ∠ABD + 150 = 180°

⇒ ∠ABD = 30°

⇒ AD = AB cos60°

⇒ AD = 4×(1/2) = 2cm …………………….(1)

⇒ BD = AB sin60°

⇒ BD = 4×(√3/2) = 2√3 cm ……………………(2)

∠B = ∠ABD + ∠CBD

⇒ 75 = 30 + ∠CBD

⇒ 45 = ∠CBD

In Δ BCD,

∠BCD = ∠CBD = 45°

CD = BD ( Sides opposite to equal angles are equal)

⇒ CD = 2√3 cm (From eq(2) ) ……………………(3)

BC = √2 BD ( ΔBCD is a right isosceles triangle)

⇒ BC = √2(2√3) = 2√6 …………………….(4)

AC = AD + DC

⇒ AC = (2 + 2√3) cm

Perimeter = AB + BC + CA

⇒ Perimeter = 4 + 2√6 + (2 + 2√3)

⇒ Perimeter = 6 + 2√6 + 2√3

Area =

⇒ Area =

⇒ Area =

⇒ Area = (2 + 2√3)(√3)

⇒ Area = (6 + 2√3) cm²