Find the equation of the circle whose centre is (2, - 5) and which passes through the point (3, 2).
The general form of the equation of a circle is:
(x - h)2 + (y - k)2 = r2
Where, (h, k) is the centre of the circle.
r is the radius of the circle.
In this question we know that (h, k) = (2, - 5), so for determining the equation of the circle we need to determine the radius of the circle.
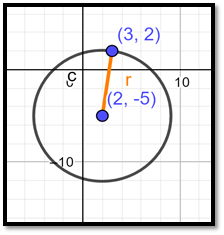
Since the circle passes through (3, 2), that pair of values for x and y must satisfy the equation and we have:
⇒ (3 - 2)2 + (2 - ( - 5))2 = r2
⇒ 12 + 72 = r2
⇒ r2 = 49 + 1 = 50
∴ r2 = 50
⇒ Equation of circle is:
(x - 2)2 + (y - ( - 5))2 = 50
⇒ (x - 2)2 + (y + 5)2 = 50
Ans:(x - 2)2 + (y + 5)2 = 50
1