Differentiate the following functions:
(i) (2x + 3) (3x – 5)
(ii) x(1 + x)3
(iii) 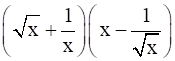
(iv) 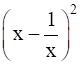
(v) 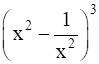
(vi) (2x2 + 5x – 1) (x – 3)
Formula:
![]()
Chain rule -
![]()
Where u and v are the functions of x.
(i) (2x + 3) (3x – 5)
Applying, Chain rule
Here, u = 2x + 3
V = 3x -5
![]() (2x + 3) (3x – 5)
(2x + 3) (3x – 5) ![]()
= (2x + 3)(3x1-1+0) + (3x – 5)(2x1-1+0)
= 6x + 9 + 6x -10
= 12x -1
(ii) x(1 + x)3
Applying, Chain rule
Here, u = x
V = (1 + x)3
![]() x(1 + x)3
x(1 + x)3![]()
= x×3×(1 + x)2 + (1 + x)3(1)
= (1 + x)2(3x+x+1)
= (1 + x)2(4x+1)
(iii) ![]() = (x1/2 + x-1)(x – x-1/2 )
= (x1/2 + x-1)(x – x-1/2 )
Applying, Chain rule
Here, u = (x1/2 + x-1)
V = (x – x-1/2 )
![]() (x1/2 + x-1)(x – x-1/2 )
(x1/2 + x-1)(x – x-1/2 )
= (x1/2 + x-1)![]() (x – x-1/2 ) + (x – x-1/2 )
(x – x-1/2 ) + (x – x-1/2 )![]() (x1/2 + x-1)
(x1/2 + x-1)
= (x1/2 + x-1)(1+ ![]() x-3/2) + (x – x-1/2 )(
x-3/2) + (x – x-1/2 )(![]() x-1/2 – x-2)
x-1/2 – x-2)
= x1/2 + x-1 + ![]() x-1 +
x-1 + ![]() x-5/2 +
x-5/2 + ![]() x1/2 – x-1 -
x1/2 – x-1 - ![]() x-1 + x-5/2
x-1 + x-5/2
= ![]() x1/2 +
x1/2 + ![]() x-5/2
x-5/2
(iv) ![]()
Differentiation of composite function can be done by
![]()
Here, f(g) = g2 , g(x) = ![]()
![]() = 2g×(1 +
= 2g×(1 + ![]() )
)
= 2(![]() (1 +
(1 + ![]() )
)
= 2(x + ![]() -
- ![]() +
+ ![]() )
)
= 2(x + ![]() )
)
(v) ![]()
Differentiation of composite function can be done by
![]()
Here, f(g) = g3 , g(x) = x2 - ![]()
![]() = 3g2×(2x -
= 3g2×(2x - ![]() )
)
= 3![]() (2x -
(2x - ![]() )
)
= 3(2x3 - ![]() -
- ![]() +
+ ![]() )
)
= 3(2x3 - ![]() +
+ ![]() )
)
(vi) (2x2 + 5x – 1) (x – 3)
Applying, Chain rule
Here, u = (2x2 + 5x – 1)
V = (x – 3)
![]() (2x2 + 5x – 1) (x – 3)
(2x2 + 5x – 1) (x – 3)
![]() (2x2 + 5x – 1)
(2x2 + 5x – 1)![]() (2x2 + 5x – 1)
(2x2 + 5x – 1)
= (2x2 + 5x – 1)×1 + (x – 3)(4x + 5)
= 2x2 + 5x – 1 + 4x2 -7x -15
= 6x2 -2x -16