Find the equation of the plane through the intersection of the planes 3x – 4y + 5z =10 and 2x + 2y - 3z = 4 and parallel to the line x = 2y = 3z.

Equation of plane through the line of intersection of planes in Cartesian form is

(1)

For the standard equation of planes in Cartesian form

So, putting in equation (1), we have

3x – 4y + 5z -10 + λ(2x + 2y - 3z - 4)=0

(3 + 2λ)x + (-4 + 2λ)y + (5-3λ)z-10-4λ=0

Given line is parallel to plane then the normal of plane is perpendicular to line,

Where A₁, B₁, C₁ are direction ratios of plane and A₂, B₂, C₂ are of line.

(3 + 2λ).6 + (-4 + 2λ).3 + (5-3λ).2=0

18 + 12λ-12 + 6λ + 10-6λ=0

16 + 12λ=0

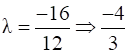
Putting the value of λ in equation (2)

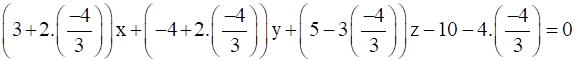
x-20y + 27z-14=0

So, required equation of plane is x-20y + 27z-14=0.