Find the Cartesian and vector equations of the planes through the line of intersection of the planes and which are at a unit distance from the origin.

Equation of plane through the line of intersection of two planes in vector form is

(1)

Where the standard equation of planes are

Putting values in equation (1)

(2)

For the equation of plane Ax + By + Cz=D and point (x1,y1,z1), a distance of a point from a plane can be calculated as

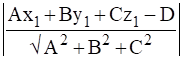
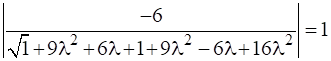
Putting value of λ in equation (2)

λ=1

λ=-1

For equations in Cartesian form put

For λ=1

x.2 + y.1 + z.(-2)-3=0

2x + y-2z-3=0

For λ=-1

x.1 + y.2 + z.(-2) + 3=0

x + 2y-2z + 3=0

In Cartesian form are 2x + y-2z-3=0 & x + 2y-2z + 3=0