Find the equation of the plane passing through the origin and perpendicular to each of the planes x + 2y - z = 1 and 3x - 4y + z = 5.

Question

Philoid · Accepted Answer

Applying condition of perpendicularity between planes,

Where A, B, C are direction ratios of plane and A₁, B₁, C₁ are of other

plane.

(1)

(2)

And plane passes through (0, 0, 0),

A(x-0) + B(y-0) + C(z-0)=0

Ax + By + Cz=0 (3)

On solving equation (1) and (2)

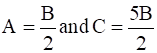
Putting values in equation(3)

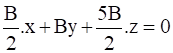
B(x + 2y + 5z)=0

x + 2y + 5z=0

So, required equation of plane is x + 2y + 5z=0.