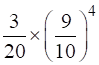In the items produced by a factory, there are 10% defective items. A sample of 6 items is randomly chosen. Find the probability that this sample contains.
(i) exactly 2 defective items
(ii) not more than 2 defective items
(iii) at least 3 defective items
(i) The probability that the item is defective = 
= p
The probability that the bulb will not fuse = 1
= 
= q
Using Bernoulli’s we have,
P(Success=x) = nCx.px.q(n-x)
x=0, 1, 2, ………n and q = (1-p), n =6
The probability that exactly 2 defective items are,
⇒ 6C2.(
)2(
)4
⇒ 
(ii) The probability that the item is defective = 
= p
The probability that the bulb will not fuse = 1
= 
= q
Using Bernoulli’s we have,
P(Success=x) = nCx.px.q(n-x)
x=0, 1, 2, ………n and q = (1-p), n =6
The probability that not more than 2 defective items are,
⇒ 6C0.(
)0(
)6 + 6C1.(
)1(
)5 + 6C2.(
)2(
)4
⇒ 
(iii) The probability that the item is defective = 
= p
The probability that the bulb will not fuse = 1
= 
= q
Using Bernoulli’s we have,
P(Success=x) = nCx.px.q(n-x)
x=0, 1, 2, ………n and q = (1-p), n =6
The probability of at least 3 defective items are,
P(3) + P(4) + P(5) + P(6)
⇒ 6C3.(
)3(
)3 + 6C4.(
)4(
)2 + 6C5.(
)5(
)1 + 6C6.(
)6(
)0
⇒ 