Find the adjoint of the given matrix and verify in each case that A. (adj A) = (adj A) =m |A|.I.
Here, 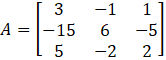
Now, we have to find adj A, and for that, we have to find co-factors:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
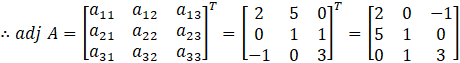
Calculating A (adj A)

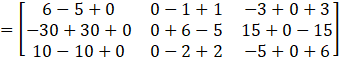

= I
Calculating (adj A)A

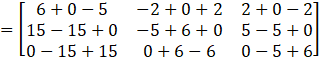
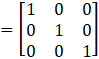
= I
Calculating |A|.I
Expanding along C1, we get
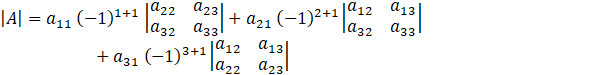
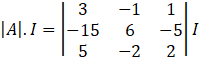
= [3(12 – 10) – (-15){-2 – (-2)} + 5(5 – 6)]I
= [3(2) + 15(0) + 5(-1)] I
= (6 – 5)I
= I
Thus, A(adj A) = (adj A)A = |A|I = I
⇒ A(adj A) = (adj A)A = |A|I
Hence Proved
Ans. 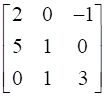
1