If A = and B = , verify that (AB)^-1 = B^-1 A^-1.

Given:

To Verify: (AB)^-1= B^-1A^-1

Firstly, we find the (AB)^-1

Calculating AB

We have to find (AB)^-1 and

Firstly, we find the adj AB and for that we have to find co-factors:

a₁₁ (co – factor of 34) = (-1)¹⁺¹(94) = (-1)²(94) = 94

a₁₂ (co – factor of 39) = (-1)¹⁺²(82) = (-1)³(82) = -82

a₂₁ (co – factor of 82) = (-1)²⁺¹(39) = (-1)³(39) = -39

a₂₂ (co – factor of 94) = (-1)²⁺²(34) = (-1)⁴(34) = 34

Now, adj AB = Transpose of co-factor Matrix

Calculating |AB|

= [34 × 94 – (82) × (39)]

= (3196 – 3198)

= -2

Now, we have to find B^-1A^-1

Calculating B^-1

Here,

We have to find A^-1 and

Firstly, we find the adj B and for that we have to find co-factors:

a₁₁ (co – factor of 6) = (-1)¹⁺¹(9) = (-1)²(9) = 9

a₁₂ (co – factor of 7) = (-1)¹⁺²(8) = (-1)³(8) = -8

a₂₁ (co – factor of 8) = (-1)²⁺¹(7) = (-1)³(7) = -7

a₂₂ (co – factor of 9) = (-1)²⁺²(6) = (-1)⁴(6) = 6

Now, adj B = Transpose of co-factor Matrix

Calculating |B|

= [6 × 9 – 7 × 8]

= (54 – 56)

= -2

Calculating A^-1

Here,

We have to find A^-1 and

Firstly, we find the adj A and for that we have to find co-factors:

a₁₁ (co – factor of 3) = (-1)¹⁺¹(5) = (-1)²(5) = 5

a₁₂ (co – factor of 2) = (-1)¹⁺²(7) = (-1)³(7) = -7

a₂₁ (co – factor of 7) = (-1)²⁺¹(2) = (-1)³(2) = -2

a₂₂ (co – factor of 5) = (-1)²⁺²(3) = (-1)⁴(3) = 3

Now, adj A = Transpose of co-factor Matrix

Calculating |A|

= [3 × 5 – 2 × 7]

= (15 – 14)

= 1

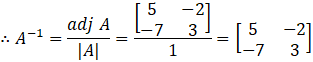
Calculating B^-1A^-1

Here,

So,

So, we get

and

∴ (AB)^-1 = B^-1A^-1

Hence verified