Show that the matrix A =  satisfies the equation
satisfies the equation
Given: ![]()
To show: Matrix A satisfies the equation x2 + 4x – 42 = 0
If Matrix A satisfies the given equation then
A2 + 4A – 42 = 0
Firstly, we find the A2
![]()
![]()
![]()
Taking LHS of the given equation .i.e.
A2 + 4A – 42
![]()
![]()
![]()
![]()
![]()
= O
= RHS
∴ LHS = RHS
Hence matrix A satisfies the given equation x2 + 4x – 42 = 0
Now, we have to find A-1
Finding A-1 using given equation
A2 + 4A – 42 = O
Post multiplying by A-1 both sides, we get
(A2 + 4A – 42)A-1 = OA-1
⇒ A2.A-1 + 4A.A-1 – 42.A-1 = O [OA-1 = O]
⇒ A.(AA-1) + 4I – 42A-1 = O [AA-1 = I]
⇒ A(I) + 4I – 42A-1 = O
⇒ A + 4I – 42A-1 = O
⇒ A + 4I – O = 42A-1
![]()
![]()
![]()
![]()
![]()
Ans. 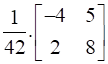 .
.
1