Find the particular solution of the differential equation dx + xdy = 0, it being given that y = when x = 1.




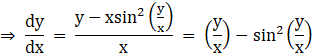
⇒ the given differential equation is a homogenous equation.


The solution of the given differential equation is :


Put y = vx






Integrating both the sides we get:




Resubstituting the value of y = vx we get



y = 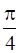when x = 1



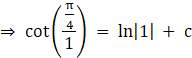
⇒ c = 1


Ans:


1
1