Find the general solution for each of the following differential equations.

Question

Philoid · Accepted Answer

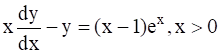
Given Differential Equation :

Formula :

i)

ii)

iii)

iv)

v) General solution :

For the differential equation in the form of

General solution is given by,

Where, integrating factor,

Answer :

Given differential equation is

Dividing above equation by x,

………eq(1)

Equation (1) is of the form

Where, and

Therefore, integrating factor is

………

General solution is

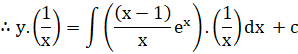
………eq(2)

Let,

Let

………

Substituting I in eq(2),

Multiplying above equation by x,

Therefore general solution is