Solve , given that when

Given Differential Equation :

Formula :

i)

ii) General solution :

For the differential equation in the form of

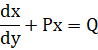
General solution is given by,

Where, integrating factor,

Answer :

Given differential equation is

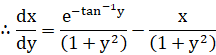
………eq(1)

Equation (1) is of the form

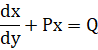
Where, and

Therefore, integrating factor is

………

General solution is

………

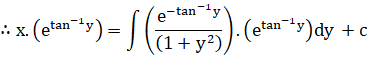
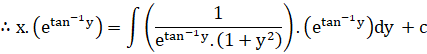
Putting x=0 and y=0

Therefore, general solution is