(a) With the help of a suitable circuit diagram, prove that the reciprocal of the equivalent resistance of a group of resistances joined in parallel is equal to the sum of the reciprocals of the individual resistors.
(b) In an electric circuit 2 resistors of 12 Ω each are joined in parallel to the a 6V battery. Find the current drawn from the battery.
OR
An electric lamp of resistance 20Ω and a conductor of resistance 4Ω are connected to a 6V battery as shown in the circuit. Calculate:
(a) The total resistance of the circuit
(b) the current through the circuit
(c) the potential difference across the
(i) the electric lamp
(ii) conductor
(d) power of the lamp.
(a) Let n resistors R1, R2 …….Rn be n resistors of resistances
R1, R2 ….Rn respectively
They are connected in parallel with a battery of emf E.
Let the current flowing across the resistor be I
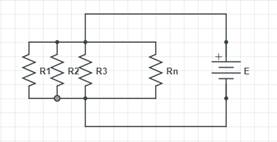
Let the equivalent resistance be Req. Then according to Ohm’s law
![]() (i)
(i)
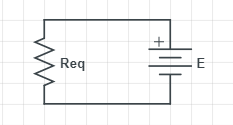
As the resistors are connected in parallel, the voltage across there ends will remain same, the current however is distributed.
For the resistor R1, let the current be I1. Then by Ohm’s law,
![]() (ii)
(ii)
Similarly
![]()
Thus, we can say that ![]()
Now the total current in the circuit will be the sum of currents through all the resistors, so
![]()
![]() (from eq (ii) and following statements)
(from eq (ii) and following statements)
Using eq (i), we can say that
![]()
Hence
![]()
Hence,the reciprocal of the equivalent resistance of a group of resistances joined in parallel is equal to the sum of the reciprocals of the individual resistors.
(b) Given:
Resistances of the resistors = 12 Ω
Emf of the battery = E = 6V
The resistors are joined in parallel with each other
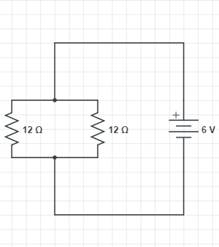
Let the net resistance be Rnet.
Let the current flowing in the circuit be I.
According to Ohm’ law, ![]() (i)
(i)
As the resistances are in parallel, Rnet is given as
![]()
![]()
∴Rnet is 6 Ω .
According to eq (i)
![]()
![]()
The current flowing in the circuit is 1 A.
OR
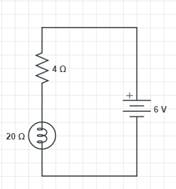
Given: Resistance of the lamp = 20 Ω
Resistance of the conductor = 4 Ω
Emf of the battery = E = 6 V
(a)The total resistance of the circuit would be simply the resistance of the series combination of bulb and the resistor.
![]()
The total resistance of the circuit is 24 Ω.
(b)The current through the circuit can be given by Ohm’s law.
Let the current in the circuit be I, then by Ohm’s law
![]()
![]()
The current in the circuit is 0.25 A.
(c) The current through the elements will be same as they are connected in series.
(i)- The potential drop across the lamp will be
![]()
![]()
(ii)- The potential drop across the conductor will be
![]()
![]()
The potential drop across the lamp is 5 V and the potential drop across the conductor is 1 V.
(d) The power of the lamp is given by
![]()
![]()
![]()
The power of the lamp is 1.25 W