Show that the lines and intersect.

Also, find their point of intersection.

Given equations :

To Find : d

Formula :

1. Cross Product :

If are two vectors

then,

2. Dot Product :

If are two vectors

then,

3. Shortest distance between two lines :

The shortest distance between the skew lines and

is given by,

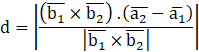
Answer :

For given lines,

Here,

Therefore,

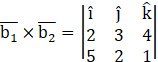
Now,

= - 15 – 18 + 33

= 0

Therefore, the shortest distance between the given lines is

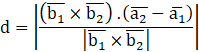
As d = 0

Hence, the given lines not intersect each other.

Now, to find point of intersection, let us convert given vector equations into Cartesian equations.

For that substituting in given equations,

General point on L1 is

x₁ = 2λ+1 , y₁ = 3λ+2 , z₁ = 4λ+3

let, P(x₁, y₁, z₁) be point of intersection of two given lines.

Therefore, point P satisfies equation of line L2.

⇒ 4λ – 6 = 15λ + 5

⇒ 11λ = -11

⇒ λ = -1

Therefore, x₁ = 2(-1)+1 , y₁ = 3(-1)+2 , z₁ = 4(-1)+3

⇒ x₁ = -1 , y₁ = -1 , z₁ = -1

Hence point of intersection of given lines is (-1, -1, -1).