Find the length and the equations of the line of shortest distance between the lines given by:
 and
and 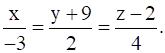
Given : Cartesian equations of lines
![]()
![]()
Formulae :
1. Condition for perpendicularity :
If line L1 has direction ratios (a1, a2, a3) and that of line L2 are (b1, b2, b3) then lines L1 and L2 will be perpendicular to each other if
![]()
2. Distance formula :
Distance between two points A≡(a1, a2, a3) and B≡(b1, b2, b3) is given by,
![]()
3. Equation of line :
Equation of line passing through points A≡(x1, y1, z1) and B≡(x2, y2, z2) is given by,
![]()
Answer :
Given equations of lines
![]()
![]()
Direction ratios of L1 and L2 are (3, -1, 1) and (-3, 2, 4) respectively.
Let, general point on line L1 is P≡(x1, y1, z1)
x1 = 3s+6 , y1 = -s+7 , z1 = s+4
and let, general point on line L2 is Q≡(x2, y2, z2)
x2 = -3t , y2 = 2t – 9 , z2 = 4t + 2
![]()
![]()
![]()
Direction ratios of ![]() are ((-3t - 3s - 6), (2t + s – 16), (4t – s – 2))
are ((-3t - 3s - 6), (2t + s – 16), (4t – s – 2))
PQ will be the shortest distance if it perpendicular to both the given lines
Therefore, by the condition of perpendicularity,
3(-3t - 3s - 6) - 1(2t + s – 16) + 1(4t – s – 2) = 0 and
-3(-3t - 3s - 6) + 2(2t + s – 16) + 4(4t – s – 2) = 0
⇒ -9t - 9s - 18 - 2t – s + 16 + 4t – s – 2 = 0 and
9t + 9s + 18 + 4t + 2s – 32 + 16t – 4s – 8 = 0
⇒ -7t – 11s = 4 and
29t + 7s = -22
Solving above two equations, we get,
t = 1 and s = -1
therefore,
P ≡ (3, 8, 3) and Q ≡ (-3, -7, 6)
Now, distance between points P and Q is
![]()
![]()
![]()
![]()
![]()
Therefore, the shortest distance between two given lines is
![]()
Now, equation of line passing through points P and Q is,
![]()
![]()
![]()
![]()
Therefore, equation of line of shortest distance between two given lines is
![]()