Find the image of the point (0, 2, 3) in the line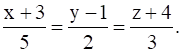

Given: Equation of line is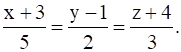

_{To find: image of point (0, 2, 3)}

Formula Used: Equation of a line is

Vector form:

Cartesian form:

where is a point on the line and with b₁ : b₂ : b₃ being the direction ratios of the line.

If 2 lines of direction ratios a₁:a₂:a₃ and b₁:b₂:b₃ are perpendicular, then a₁b₁+a₂b₂+a₃b₃ = 0

_{Mid-point of line segment joining (}x₁, y₁, z₁) and (x₂, y₂, z₂) is

_Explanation:

Let

So the foot of the perpendicular is (5λ – 3, 2λ + 1, 3λ – 4)

The direction ratios of the perpendicular is

(5λ – 3 - 0) : (2λ + 1 - 2) : (3λ - 4 - 3)

⇒ (5λ – 3) : (2λ – 1) : (3λ – 7)

Direction ratio of the line is 5 : 2 : 3

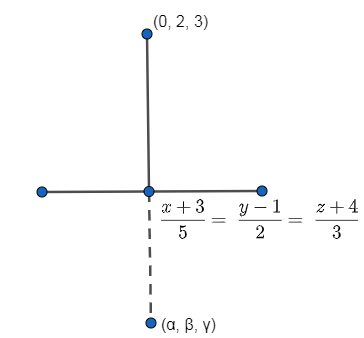
From the direction ratio of the line and the direction ratio of its perpendicular, we have

5(5λ - 3) + 2(2λ – 1) + 3(3λ – 7) = 0

⇒ 25λ – 15 + 4λ – 2 + 9λ – 21 = 0

⇒ 38λ = 38

⇒ λ = 1

So, the foot of the perpendicular is (2, 3, -1)

The foot of the perpendicular is the mid-point of the line joining (0, 2, 3) and (α, β, γ)

So, we have

So, the image is (4, 4, -5)