Find two positive numbers whose sum is 16 and the sum of whose squares is minimum.

Given,

• The two numbers are positive.

• the sum of two numbers is 16.

• the sum of the squares of two numbers is minimum.

Let us consider,

• x and y are the two numbers, such that x > 0 and y > 0

• Sum of the numbers : x + y = 16

• Sum of squares of the numbers : S = x² + y²

Now as,

x + y = 16

y = (16-x) ------ (1)

Consider,

S = x² + y²

By substituting (1), we have

S = x² + (16-y)² ------ (2)

For finding the maximum/ minimum of given function, we can find it by differentiating it with x and then equating it to zero. This is because if the function f(x) has a maximum/minimum at a point c then f’(c) = 0.

Differentiating the equation (2) with x

----- (3)

[Since ]

Now equating the first derivative to zero will give the critical point c.

So,

⇒ 2x – 2(16 -x) = 0

⇒ 2x – 32 + 2x = 0

= 4x = 32

⇒ x = 8

As x > 0, x = 8

Now, for checking if the value of S is maximum or minimum at x=8, we will perform the second differentiation and check the value of at the critical value x = 8.

Performing the second differentiation on the equation (3) with respect to x.

[Since and ]

Now when x = 8,

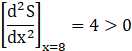
As second differential is positive, hence the critical point x = 8 will be the minimum point of the function S.

Therefore, the function S = sum of the squares of the two numbers is minimum at x = 8.

From Equation (1), if x= 8

y = 16 – 8 = 8

Therefore, x = 8 and y = 8 are the two positive numbers whose su is 16 and the sum of the squares is minimum.