The rate of working of an engine is given by.
and υ is the speed of the engine. Show that R is the least when υ = 20.
Given:
Rate of working of an engine R, v is the speed of the engine:
, where 0<v<30
For finding the maximum/ minimum of given function, we can find it by differentiating it with v and then equating it to zero. This is because if the function f(x) has a maximum/minimum at a point c then f’(c) = 0.
Now, differentiating the function R with respect to v.
----- (1)
[Since 
and 
]
Equating equation (1) to zero to find the critical value.
v2 = 400
v = 20 (or) v = -20
As given in the question 0<v<30, v = 20
Now, for checking if the value of R is maximum or minimum at v=20, we will perform the second differentiation and check the value of 
at the critical value v = 20.
Differentiating Equation (1) with respect to v again:
[Since 
and 
]
----- (2)
Now find the value of 
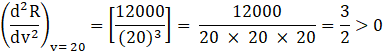
So, at critical point v = 20. The function R is at its minimum.
Hence, the function R is at its minimum at v = 20.