An open box with a square base is to be made out of a given cardboard of area (square) units. Show that the maximum volume of the box is (cubic) units.

Given,

• The open box has a square base

• The area of the box is c² square units.

• The volume of the box is maximum.

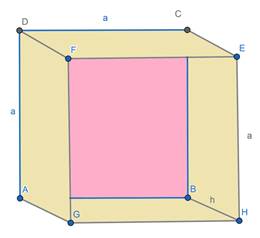
Let us consider,

• The side of the square base of the box be ‘a’ units. (pink coloured in the figure)

• The breadth of the 4 sides of the box will also be ‘a’units (skin coloured part).

• The depth of the box or the length of the sides be ‘h’ units (skin coloured part).

Now, the area of the box =

(area of the base) + 4 (area of each side of the box)

So as area of the box is given c²,

c² = a² + 4ah

---- (1)

Let the volume of the newly formed box is :

V = (a)² × (h)

[substituting (1) in the volume formula]

------ (2)

For finding the maximum/ minimum of given function, we can find it by differentiating it with a and then equating it to zero. This is because if the function f(a) has a maximum/minimum at a point c then f’(c) = 0.

Differentiating the equation (2) with respect to a:

------- (3)

[Since ]

To find the critical point, we need to equate equation (3) to zero.

c² – 3a² = 0

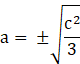
[as ‘a’ cannot be negative]

Now to check if this critical point will determine the maximum Volume of the box, we need to check with second differential which needs to be negative.

Consider differentiating the equation (3) with x:

----- (4)

[Since ]

Now let us find the value of

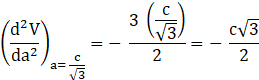
As , so the function V is maximum at

Now substituting a in equation (1)

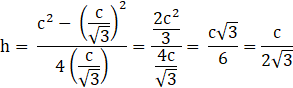
Therefore side of wanted box has a base side, is and height of the box, .

Now, the volume of the box is