A wire of length 36 cm is cut into two pieces. One of the pieces is turned in the form of a square and the other in the form of an equilateral triangle. Find the length of each piece so that the sum of the areas of the two be minimum.

Given,

• Length of the wire is 36 cm.

• The wire is cut into 2 pieces.

• One piece is made to a square.

• Another piece made into a equilateral triangle.

Let us consider,

• The perimeter of the square is x.

• The perimeter of the equilateral triangle is (36-x).

• Side of the square is

• Side of the triangle is

Let the Sum of the Area of the square and triangle is

--- (1)

For finding the maximum/ minimum of given function, we can find it by differentiating it with x and then equating it to zero. This is because if the function A(x) has a maximum/minimum at a point c then A’(c) = 0.

Differentiating the equation (1) with respect to x:

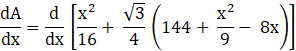
[Since ]

----- (2)

To find the critical point, we need to equate equation (2) to zero.

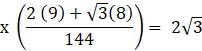
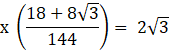
Now to check if this critical point will determine the minimum area, we need to check with second differential which needs to be positive.

Consider differentiating the equation (3) with x:

----- (4)

[Since ]

Now let us find the value of

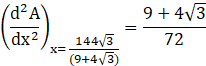
As , so the function A is minimum at

Now, the length of each piece is and