Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are 
of the corresponding sides of the first triangle.
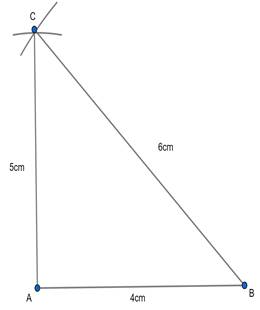
Step 1 Draw a line segment AB = 4 cm.
Step 2: Taking point A as center, draw and arc of 5 cm radius. Similarly, taking point B as its center, draw an arc of 6 cm radius. These arcs will intersect each other at point C. Now, AC = 5 cm and BC=6 cm
And △ABC is the required triangle.
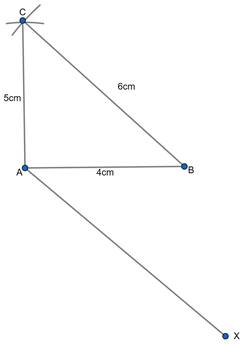
Step 3: Draw a ray AX making an acute angle with line AB on the opposite site of vertex C.
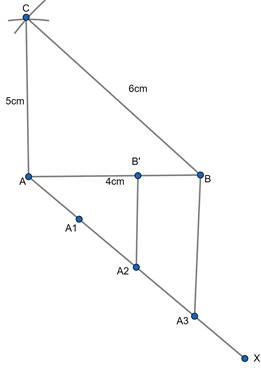
Step 4: Locate 3 points (as 3 is greater between 2 and 3) online AX such that AA1=A1A2=A2A3.
Step 5: Join BA3 and draw a line through A2 parallel to BA3 to intersect AB at point B′.
Step 6: Draw a line through B′ parallel to the line BC to intersect AC at C′ △AB′C′ is the required triangle.
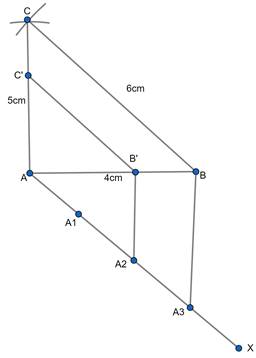
Justification
∠A = ∠A (Common)
∠C=∠C' and ∠B=∠B
(Corresponding angles)
Thus ∆ AB' C'~ ∆ABC
by AAA similarility condition
From the figure,
