Draw a right triangle in which the sides (other than hypotenuse) are of lengths 5 cm and 4 cm. Then construct another triangle whose sides are 5/3 times the corresponding sides of the given triangle.

Question

Philoid · Accepted Answer

The steps involved in the required construction are:

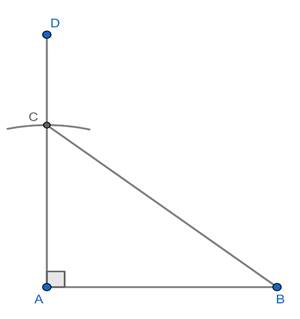
1) Draw a line segment AB=5 cm.

2) Using a protractor, draw ∠BAD=90°. Taking A as the center and radius 4 cm, draw an arc, intersecting AD at C. Join BC.

3) Draw any line segment AE, making an acute angle with AB and opposite to the vertex C. Taking A as the center and any radius, draw an arc, intersecting AE at F. Taking F as the center and radius AF, draw an arc, intersecting AE at G. Similarly, repeat the process 3 more times to get points H, I and J. Join BH.

4) Taking H as the center and any radius, draw an arc., intersecting AE and BH at K and L respectively. Taking J as the center and radius HK, draw an arc, intersecting AE at M. Taking M as the center and radius KL, draw an arc, intersecting previous arc at N. Join and extend JN, intersecting extended AB at O.

5) Taking B as the center and any radius, draw an arc., intersecting BA and BC at Q and R respectively. Taking O as the center and radius BQ, draw an arc., intersecting AO at S. Taking S as the center and radius QR, draw an arc, intersecting previous arc at T. Join and extend OT, intersecting AD at P.

6) ∆AOP is the required triangle.