Determine the area enclosed by curve y=x3, and the lines y=0, x=2 and x=4.
Given the boundaries of the area to be found are,
• The curve y = x3
• The y= 0, x-axis
• x = 2 (a line parallel toy-axis)
• x = 4 (a line parallel toy-axis)
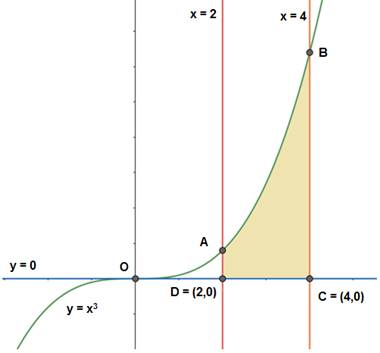
As per the given boundaries,
• The curve y = x3 is a curve with vertex at (0,0).
• x=2 is parallel toy-axis at 2 units away from the y-axis.
• x=4 is parallel toy-axis at 4 units away from the y-axis.
• The four boundaries of the region to be found are,
•Point A, where the curve y = x3 and x=2 meet.
•Point B, where the curve y = x3 and x=4 meet.
•Point C, where the x-axis and x=4 meet i.e. C(4,0).
•Point D, where the x-axis and x=2 meet i.e. D(2,0).
Area of the required region = Area of ABCD.
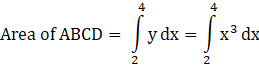
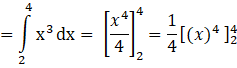
[Using the formula ![]() ]
]
![]()
= 60 sq. units
The Area of the required region = 60 sq. units.