Determine the area under the curve y= , included between the lines x=0 and x=4.

Question

Philoid · Accepted Answer

Given the boundaries of the area to be found are,

• The curve

• x = 0 (y-axis)

• x = 4 (a line parallel toy-axis)

Here the curve, , can be re-written as

----- (1)

This equation (1) represents a circle equation with (0,0) as center and, a units as radius.

As x and y have even powers, the given curve will be about the x-axis and y-axis.

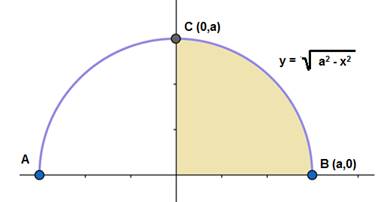
As per the given boundaries,

• The curve, is a curve with vertex at (0,0).

• x=4 is parallel toy-axis at 4 units away from the y-axis. (but this might not really effect the boundaries as the value of ‘a’ in the equation is unknown.)

• x=0 is the y-axis.

Area of the required region = Area of OBC.

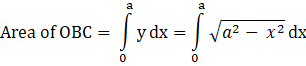
[Using the formula, ]

[sin^-1(1) = 90° and sin^-1(0) = 0° ]

The Area of the required region

Determine the area under the curve y=, included between the lines x=0 and x=4.