Using integration, find the area of the region bounded between the line x=2 and the parabola y2=8x.
Given the boundaries of the area to be found are,
• The parabola y2 = 8x
• x = 2 (a line parallel toy-axis)
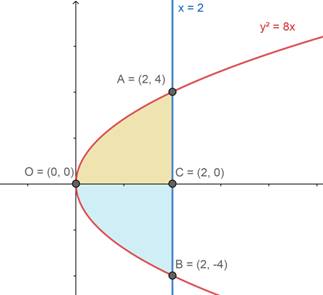
As per the given boundaries,
• The curve y2 =8x, has only the positive numbers as y has even power, so it is about the x-axis equally distributed on both sides as the vertex is at (0,0).
• x= 2 is parallel toy-axis which is 2 units away from the y-axis.
The boundaries of the region to be found are,
•Point A, where the curve y2 = 8x and x=2 meet which has positive y.
•Point B, where the curve y2 = 8x and x=2 meet which has negative y.
•Point C, where the x-axis and x=2 meet i.e. C(2,0).
Area of the required region = Area under OACB.
But,
Area under OACB = Area under OAC + Area under OBC
This can also be written as,
Area under OACB = 2 × Area under OAC
[area under OAC = area under OBC as AOB is symmetrical about the x-axis.]
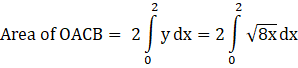
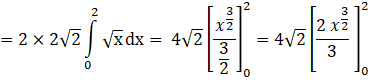
[Using the formula ![]() ]
]
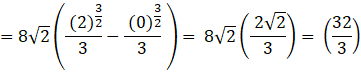
![]()
The Area of the required region ![]()