Compare the areas under the curves y=cos²x and y=sin²x between x=0 and x=π.

Given

• First curve y = cos² x

• Second curve y = sin² x

• x= 0

• x= π

Consider the curve y = cos² x

Now consider the y values for some random x values between 0 and π for the function y = cos² x.

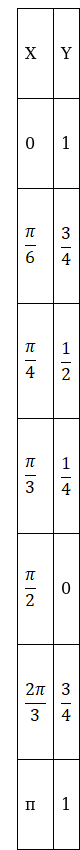
From the table we can clearly draw the graph for y = cos² x

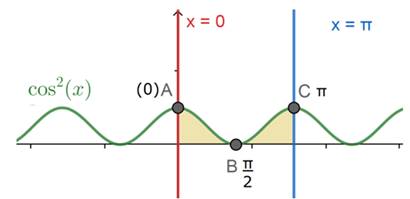
The required area under the curve is given by:

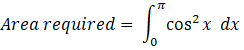
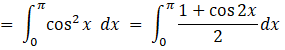
[using the property cos 2x = 2 cos² x - 1]

[using the formula, ]

[as sin 2π = 0, sin 0 = 0]

Hence the required area of the curve y = cos² x from x = 0 to x=π is sq. units. ------ (1)

Consider the curve y = sin² x

Now consider the y values for some random x values between 0 and π for the function y = sin² x.

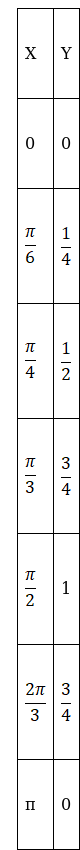
From the table we can clearly draw the graph for y = sin² x

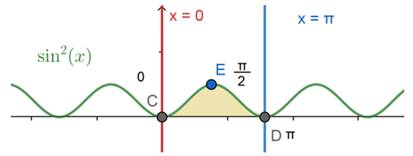
The required area under the curve is given by:

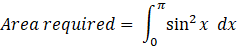
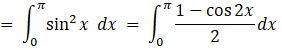
[using the property cos 2x = 1- 2 sin² x]

[using the formula, ]

[as sin 2π = 0, sin 0 = 0]

Hence the required area of the curve y = sin² x from x = 0 to x=π is sq. units. ----- (2)

From (1) and (2), we can clearly state that, the areas under

y = cos² x and y = sin² x are similar which is sq. units.