Find the area bounded by the curve y=cos x between x=0 to x=2π.

_Given

• Curve is y = cos x

• x = 0 and

• x = 2π

The given curve is y = cos x.

Now consider the y values for some random x values between 0 and 2π for the function y = cos x.

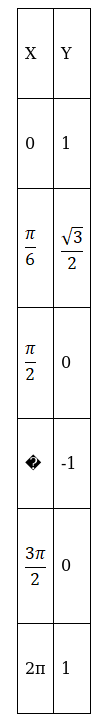
From the table we can clearly draw the graph for y = cos x

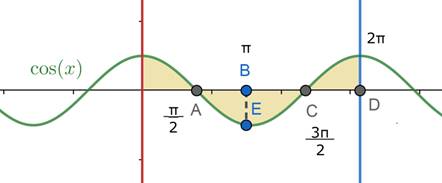
From the given curve, we can say that,

For , y = cos x

For , y = -cos x

For , y = cos x

The required area under the curve is given by:

Area required = Area under of OA + Area of ABC + Area under AC

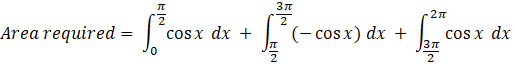
[using the formula, ]

[as , sin 2π = 0, , sin 0 = 0]

Hence the required area of the curve y = cos x from x = 0 to x=2π is 4 sq. units.