(a) Draw the equipotential surfaces corresponding to a uniform electric field in the z-direction.

(b) Derive an expression for the electric potential at any point along the axial line of an electric dipole.

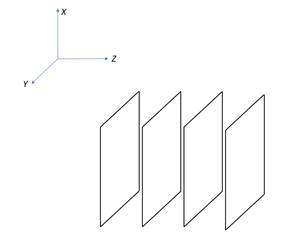
(a)

Note that the electric field is always perpendicular to the equipotential surface. Hence, the equipotential surfaces are going to be infinite plane sheets parallel to the x-y plane.

Also, the electric field strength is proportional to the distance between the surfaces. Hence, the surfaces will be evenly spaced.

(b)

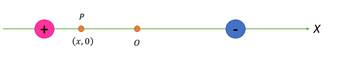
Let charge +q and -q be separated by distance 2a. Let origin be at the centre of the two charges. Consider any arbitrary point P (x,0).

Let r_a be the distance of point P from the positive charge and r_b be the distance of the point P from the negative charge.

The electric potential at point P is given by:

We have two cases:

Case I: and

Now,

and

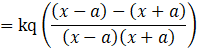
Case II: and

Now,

and

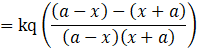
Case III: and

Now,

and

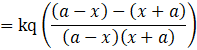
Case IV:

and
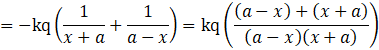