Find the value of λ such that the line is perpendicular to the plane 3x - y – 2z = 7.

Given :

Equation of line :

Equation of plane : 3x – y – 2z = 7

To Find :

Formulae :

1) Parallel vector to the line :

If equation of the line is then,

Vector parallel to the line is given by,

2) Normal vector to the plane :

If equation of the plane is ax + by + cz = d then,

Vector normal to the plane is given by,

3) Cross Product :

If are two vectors

then,

Answer :

For given equation of line,

Parallel vector to the line is

For given equation of plane,

3x – y – 2z = 7

normal vector to the plane is

As given line and plane are perpendicular to each other.

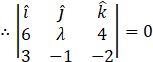
Comparing coefficients of on both sides

3λ = -6

λ = -2