Find the value of λ for which the line

is parallel to the plane

Given :

Equation of line :

Equation of plane :

To Find : λ

Formulae :

1) Parallel vector to the line :

If equation of the line is then,

Vector parallel to the line is given by,

2) Angle between a line and a plane :

If Ө is a angle between the line and the plane , then

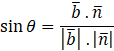
Where, is vector parallel to the line and

is the vector normal to the plane.

Answer :

For given equation of line,

Parallel vector to the line is

For given equation of plane,

normal vector to the plane is

Therefore, angle between given line and plane is

As given line is parallel too the given plane, angle between them is 0.

4 + 9 + 4 λ = 0

13 + 4λ = 0

4λ = -13