Find the vector and Cartesian equations of a plane which is at a distance of from the origin and whose normal vector from the origin is

Given :

To Find : Equation of a plane

Formulae :

1) Unit Vector :

Let be any vector

Then the unit vector of is

Where,

2) Dot Product :

If are two vectors

then,

3) Equation of plane :

Equation of plane which is at a distance of 5 units from the origin and having as a unit vector normal to it is

Where,

For given normal vector

Unit vector normal to the plane is

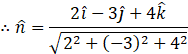
Equation of the plane is

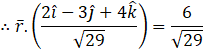
This is a vector equation of the plane.

Now,

= (x × 2) + (y × (-3)) + (z × 4)

= 2x - 3y + 4z

Therefore equation of the plane is

2x - 3y + 4z = 6

This is the Cartesian equation of the plane.