Find the equation of a plane which is at a distance of 3√3 units from the origin and the normal to which is equally inclined to the coordinate axes.

Given :

To Find : Equation of plane

Formulae :

1) Distance of plane from the origin :

If is the vector normal to the plane, then distance of the plane from the origin is

Where,

2)

Where

3) Equation of plane :

If is the vector normal to the plane, then equation of the plane is

As

⇒ l = m = n

Therefore equation of normal vector of the plane having direction cosines l, m, n is

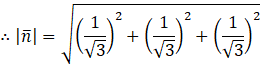
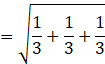
= √1

= 1

Now,

distance of the plane from the origin is

Therefore equation of required plane is

This is the required equation of the plane.