A toy company manufactures two types of dolls, A and B. Each doll of type B take twice as long to produce as one of type A, and the company would have time to make a maximum of 2000 per day, if it produces only type A. the supply of plastic is sufficient to produce 1500 dolls per day (both A and B combined ). Type B requires a fancy dress of which there are only 600 per day available. If the company makes profit of ₹3 and ₹5 per dolls respectively on dolls A and B, how many of each should be produced per day in order to maximize the profit? Also, find the maximum profit.
Let x and y be number of doll A manufactured and doll B manufactured.
∴According to the question,
x + y 
1500, x + 2y 
y
Maximize Z = 3x + 5y
The feasible region determined by x + y 
1500, x + 2y 
y
is given by
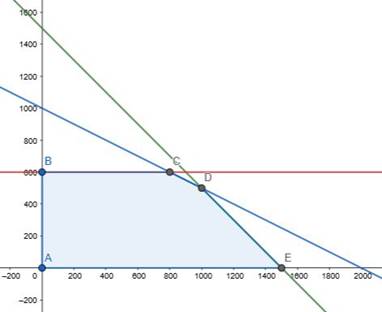
The corner points of feasible region are A(0,0) , B(0,600) , C(800,600),D(1000,500),E(1500,0).
The value of Z at corner points are
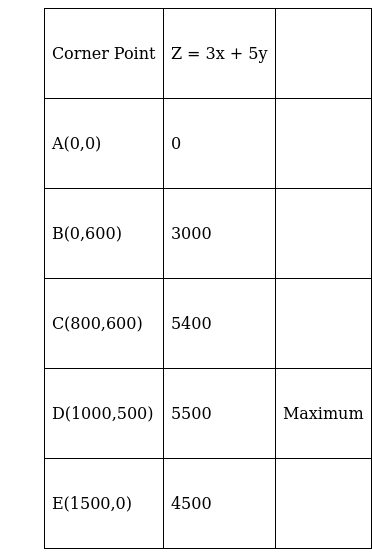
The maximum value of Z is 5500 at point (1000,500).
Hence, the manufacturer should produce 1000 types of doll A and 500 types of doll B to make maximum profit of Rs.5500.