Let’s see the pictures in the graph paper below and find the area of the figures and note it down.
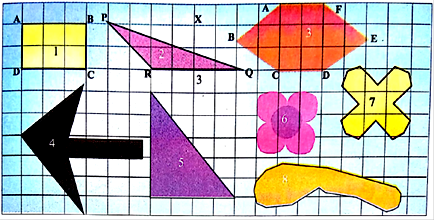

Since pictures are laid on a graph paper, a bar in graph paper has a measure of 1 unit (Here, 1 bar = 1 cm) and is square in shape.
Using the information that, 1 bar = 1 cm and square in shape.
For shape 1:
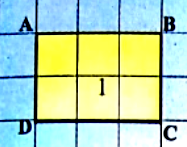
We need to find the number of complete smallest square regions enclosed by the figure.
Complete smallest square regions is equal to 1 bar of the graph.
Note that, in the figure
There are 6 bars enclosed by the figure.
These 6 bars are completely enclosed within the boundary of the figure.
⇒ There are 6 number of complete smallest square regions enclosed by the figure.
We need to find number of half of smallest square regions enclosed by the figure.
As we already know that, 6 complete square regions are enclosed by the figure 1. There are no other regions enclosed by the figure other than these 6 squares.
⇒ There are 0 number of half of smallest square regions enclosed by the figure.
We need to find number of more than half of smallest square regions enclosed by the figure.
There are no square (be it half or more than half) regions enclosed by the figure than the 6 complete square regions.
⇒ There are 0 number of more than half of smallest square regions enclosed by the figure.
We need to find number of less than half of smallest square regions enclosed by the figure.
There are no square (be it half, more than half or less than half) regions enclosed by the figure than the 6 complete square regions.
⇒ There are 0 number of less than half of smallest square regions enclosed by the figure.
Now, we need to find the total area of the figure, given that area of one smallest square region is 1 cm2.
From the previous data, we can conclude that
Complete smallest square regions = 6
As,
Area of 1 smallest square region = 1 cm2
Then, area of 6 smallest square regions = 6 × 1 cm2
⇒ Area of 6 smallest square regions = 6 cm2
Hence, we have taken out the data of shape 1.
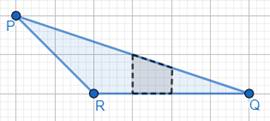
For shape 2:
We need to find number of complete smallest square regions enclosed by the figure.
Complete smallest square regions is equal to 1 bar of the graph.
Note that, in the figure
There are many regions, some are half of a bar while some are more than or less than half of a bar.
But there is only one complete bar.
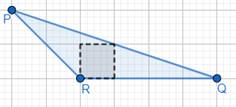
This 1 bar is completely enclosed by the figure.
⇒ There is only 1 complete smallest square region enclosed by the figure.
We need to find number of half of smallest square regions enclosed by the figure.
Out of all regions enclosed by the figure, there are only 3 regions which are half of square.
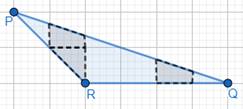
These 3 bars are completely enclosed by the figure.
⇒ There are 3 half of smallest square regions enclosed by the figure.
We need to find number of more than half of smallest square regions enclosed by the figure.
Apart from 1 complete square region and 3 half square regions, we can note that there is only 1 region which is more than half of square but less than a complete square.
This 1 bar is completely enclosed by the figure too.
⇒ There is 1 more than half of smallest square region enclosed by the figure.
We need to find number of less than half of smallest square regions enclosed by the figure.
Apart from 1 complete square region, 3 half square regions and 1 more than half square region, we can note that there are 3 regions which are less than half of square.
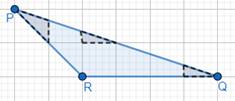
These 3 bars are completely enclosed by the figure.
⇒ There are 3 less than half of smallest square regions enclosed by the figure.
Now, we need to find the total area of the figure, given that area of one smallest square region is 1 cm2.
To find area of the figure, enclose the figure into a rectangle or square (whichever is possibly fit).
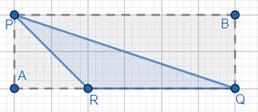
Here, we have a rectangle, PBQA.
We need to find the area of this rectangle.
Area of this rectangle = number of complete bars × 1 cm2 [∵, 1 cm2 is the area of 1 bar]
Number of complete bars in this rectangle are 12.
So,
Area of rectangle = 12 × 1 cm2
⇒ Area of PBQA = 12 cm2 …(i)
Now, there are 2 right angled triangles apart from the shape 2 enclosed in this rectangle.
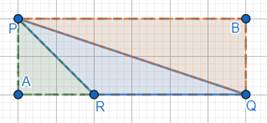
We have right-angled triangles namely, ∆PBQ and ∆PAR.
We can find area of these two triangles.
Area of triangle is given by,
![]()
For ∆PBQ,
∠PBQ = 90°
Base = PB
∵ 1 side of each 6 bars cover length PB
⇒ PB = 6 cm (length of one side of a bar = 1 cm)
⇒ Base = 6 cm
Height = BQ
∵ 1 side of each 2 bars cover length BQ
⇒ BQ = 2 cm (length of one side of a bar = 1 cm)
⇒ Height = 2 cm
Thus,
![]()
⇒ Area of ∆PBQ = 6 cm2 …(ii)
For ∆PAR,
∠PAR = 90°
Base = RA
∵1 side of each 2 bars cover the length RA
⇒ RA = 2 cm (length of one side of a bar = 1 cm)
⇒ Base = 2 cm
Height = PA
∵ 1 side of each 2 bars cover the length PA
⇒ PA = 2 cm (length of one side of a bar = 1 cm)
⇒ Height = 2 cm
Thus,
![]()
⇒ Area of ∆PAR = 2 cm2 …(iii)
Add these two triangles’ area, then subtract from the area of the rectangle. We have
Area of shape 2 = Area of PBQA – (Area of ∆PBQ + Area of ∆PAR)
⇒ Area of shape 2 = 12 – (6 + 2) [from (i), (ii) & (iii)]
⇒ Area of shape 2 = 12 – 8
⇒ Area of shape 2 = 4 cm2
Hence, we have taken out the data of shape 2.
For shape 3:
We need to find number of complete smallest square regions enclosed by the figure.
Complete smallest square regions is equal to 1 bar of the graph.
Note that, in the figure
There are 8 complete squares enclosed by the figure.
⇒ There are 8 complete smallest square regions enclosed by the figure.
We need to find number of half of smallest square regions enclosed by the figure.
Apart from 8 complete square regions, we can note that there are 2 regions which are (approx.) half of square.
The small extra region can be ignored.
⇒ There are 2 half of smallest square regions enclosed by the figure.
We need to find number of more than half of smallest square regions enclosed by the figure.
Apart from 8 complete square regions and 2 half square regions, we can note that there are 4 regions which are more than half of square region.
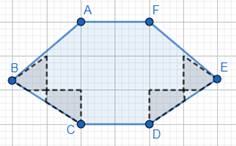
⇒ There are 4 more than half of smallest square regions enclosed by the figure.
We need to find number of less than half of smallest square regions enclosed by the figure.
Apart from 8 complete square regions, 2 half square regions and 4 more than half of square regions, we can note that there are 2 regions which are less than half of square region.
⇒ There are 2 less than half of smallest square regions enclosed by the figure.
Now, we need to find the total area of the figure, given that area of one smallest square region is 1 cm2.
To find area of the figure, enclose the figure into a rectangle or square (whichever is possibly fit).
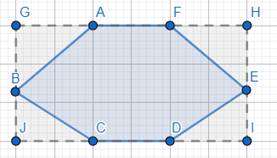
Here, we have a rectangle, GHIJ.
We need to find the area of this rectangle.
Area of this rectangle = number of complete bars × 1 cm2 [∵, 1 cm2 is the area of 1 bar]
Number of complete bars in this rectangle are 18.
So,
Area of rectangle = 18 × 1 cm2
⇒ Area of GHIJ = 18 cm2 …(i)
Now, there are 4 right angled triangles apart from the shape 3 enclosed in this rectangle.
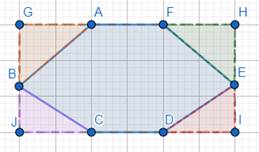
We have right-angled triangles namely, ∆AGB, ∆FHE, ∆EID and ∆BJC.
We can find area of these four triangles.
Area of triangle is given by,
![]()
For ∆AGB,
∠AGB = 90°
Base = BG
[∵, 1 side of one bar and 4/5th side of another bar covers BG ⇒ ![]() (length of one side of a bar = 1 cm, so length of fourth part of a side of a bar = 4/5 since the bar has 5 divisions)]
(length of one side of a bar = 1 cm, so length of fourth part of a side of a bar = 4/5 since the bar has 5 divisions)]
![]()
Height = AG
[∵, 1 side of each 2 bars cover length AG ⇒ AG = 2 cm (length of one side of a bar = 1 cm)]
⇒ Height = 2 cm
Thus,
![]()
![]() …(ii)
…(ii)
Similarly,
For ∆FHE,
∠FHE = 90°
![]() …(iii)
…(iii)
For ∆BJC,
∠BJC = 90°
Base = JC
[∵, 1 side of each 2 bars cover the length JC ⇒ RA = 2 cm (length of one side of a bar = 1 cm)]
⇒ Base = 2 cm
Height = BJ
[∵, 1 side of each one bar and 1/5th side of another bar covers BJ ⇒ ![]() (length of one side of a bar = 1 cm)]
(length of one side of a bar = 1 cm)]
![]()
Thus,
![]()
![]() …(iv)
…(iv)
Similarly,
For ∆EID,
∠EID = 90°
![]() …(v)
…(v)
Add these four triangles’ area, then subtract from the area of the rectangle. We have
Area of shape 3 = Area of GHIJ – (Area of ∆AGB + Area of ∆FHE + Area of ∆BJC + Area of ∆EID)
![]() [from (i), (ii), (iii) & (iv)]
[from (i), (ii), (iii) & (iv)]
![]()
⇒ Area of shape 3 = 18 – 6
⇒ Area of shape 3 = 12 cm2
Hence, we have taken out the data of shape 3.
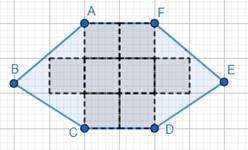
For shape 4:
Let the figure be ABCDEFG.
We need to find number of complete smallest square regions enclosed by the figure.
Complete smallest square regions is equal to 1 bar of the graph.
Note that, in the figure
There are many regions, some are half of a bar while some are more than or less than half of a bar.
But there is only one complete bar.
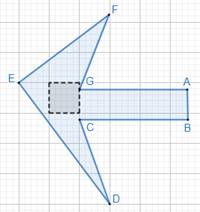
⇒ There is 1 complete smallest square region enclosed by the figure.
We need to find number of half of smallest square regions enclosed by the figure.
Apart from 1 complete square region, we can see only 1 region that looks like half of a square region.
⇒ There is 1 half of smallest square region enclosed by the figure.
We need to find number of more than half of smallest square regions enclosed by the figure.
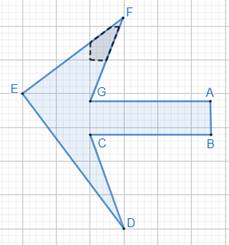
Apart from 1 complete square region and 1 half of square region, we can see 7 regions that are more than half of smallest square regions enclosed by the figure.
⇒ There are 7 more than half of smallest square regions.
We need to find number of less than half of smallest square regions enclosed by the figure.
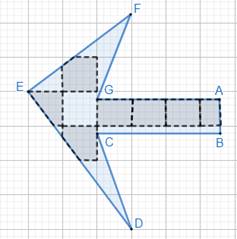
Apart from 1 complete square region, 1 half of square region and 7 more than half of square region, we can see 11 less than half of square regions.
The rest of the region less than half of a square is the region we are looking for. Neglect the regions which has negligible area.
⇒ There are 11 less than half of smallest square regions enclosed by the figure.
Now, we need to find the total area of the figure, given that area of one smallest square region is 1 cm2.
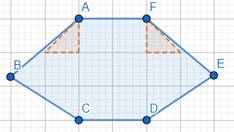
To find area of the figure, divide the figure into possible general figures as follows:
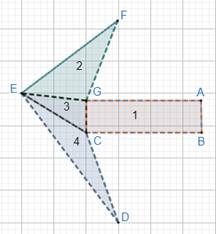
See figure 1: It is a rectangle, ABCG.
Area of this rectangle is determined by the number of bars it encloses.
So, figure 1 encloses 3 complete bars and 1 half bar.
∵, area of 1 complete bar = 1 cm2
![]()
Then,
Area of 3 complete bars = 3 × 1 = 3 cm2
Area of ABCG = Area of 3 complete bars + Area of 1 half bar
![]()
![]()
![]() …(i)
…(i)
See figure 2: It is a triangle, FEG.
Area of triangle is given by
![]()
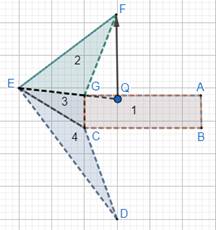
Here, base = EG
And height is given by the arrow, QF.
EG = 2 cm [∵, one side of each 2 bars cover distance of EG, and length of a side of a bar = 1 cm ⇒ Length of side of 2 bars = 2 cm]
⇒ Base = 2 cm
2 complete bars and 3/5th part of a bar cover the distance QF.
![]()
![]()
![]()
![]()
Thus,
![]()
![]() …(ii)
…(ii)
See figure 3: It is a triangle, EGC.
Area of triangle is given by
![]()
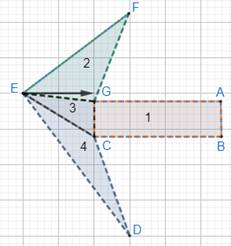
Here, base = CG
And height is given by the arrow.
One side of 1 bar covers the distance of CG, and length of side of a bar = 1 cm.
Then, CG = 1 cm
⇒ Base = 1 cm
And one side of each 2 bars cover the distance of height.
⇒ Height = 2 cm
![]()
⇒ Area of ∆EGC = 1 cm2 …(iii)
Further dividing figure 4 into 4 and 5.
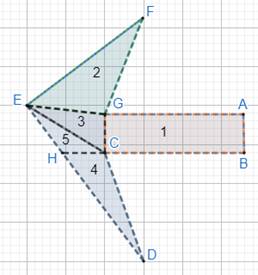
For figure 4: We have the triangle, CHD.
Area of triangle is given by
![]()
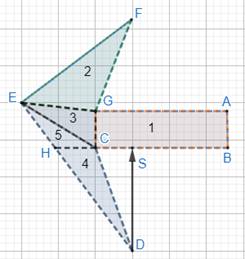
Here, base = HC
One side of complete bar and 1/5th part of side of another bar covers the distance HC.
If length of a side of complete bar = 1 cm
Then,
![]()
![]()
![]()
![]()
![]()
Height = DS
One side of each 2 complete bars and 4/5th part of side of a bar covers the distance DS.
![]()
![]()
![]()
![]()
Thus,
![]()
![]() …(iv)
…(iv)
For figure 5: We have triangle, EHC.
Area of triangle is given by
![]()
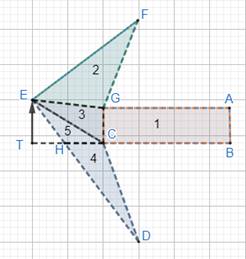
Here, base = HC
As we know,
![]()
![]()
Height = TE
One side of a complete bar and 1/5th part of side of a bar covers distance of TE.
![]()
![]()
![]()
![]()
Thus,
![]()
![]() …(v)
…(v)
∴, Area of the whole figure = Area of figure 1 + Area of figure 2 + Area of figure 3 + Area of figure 4 + Area of figure 5
![]()
[from (i), (ii), (iii), (iv) & (v)]
![]()
![]()
⇒ Area of whole figure = 9.5 cm2
Thus,
Area of shape 4 = 9.5 cm2
Hence, we have taken out the data of shape 4.
For shape 5:
Let the figure be ABC.
We need to find number of complete smallest square regions enclosed by the figure.
Complete smallest square regions is equal to 1 bar of the graph.
Note that, in the figure
There are many regions, some are half of a bar while some are more than or less than half of a bar.
But there are 6 complete bars.
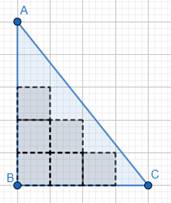
⇒ There are 6 complete smallest square regions enclosed by the figure.
We need to find number of half of smallest square regions enclosed by the figure.
Apart from 6 complete bars, we can see that there is just one nearly half of the square.
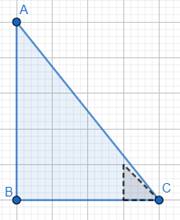
⇒ There is 1 half of the smallest square regions enclosed by the figure.
We need to find number of more than half of smallest square regions enclosed by the figure.
Apart from 6 complete square region and 1 half of square region, we can see 3 more than half of square region.
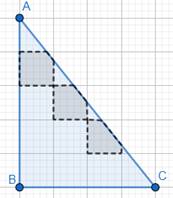
⇒ There are 3 more than half of smallest square region enclosed by the figure.
We need to find number of less than half of smallest square region enclosed by the figure.
Apart from 6 complete square region, 1 half of square region and 3 more than half of square region, we can see 3 less than half of square region.
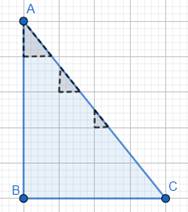
⇒ There are 3 less than half of smallest square region enclosed by the figure.
Now, we need to find the total area of the figure, given that area of one smallest square region is 1 cm2.
To find area of the figure:
Since, this figure is ∆ABC.
![]()
![]()
Since, sides of each four bars cover distance BC, and length of 1 side of a bar = 1 cm.
⇒ Length of BC = 4 × 1
⇒ Length of BC = 4 cm
Sides of each five bars cover distance AB, and length of 1 side of a bar = 1 cm.
⇒ Length of AB = 5 × 1
⇒ Length of AB = 5 cm
Thus,
![]()
⇒ Area of ∆ABC = 2 × 5
⇒ Area of ∆ABC = 10 cm2
Hence, we have taken out the data of shape 5.
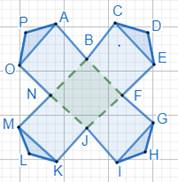
For shape 6:
We have from the question:

We need to find the number of complete smallest square region enclosed by the figure.
Here, either we can draw the figure by hand on a graph paper, or we need to imagine the bar lines which are missing behind the rigid figure.
Clearly, the figure encloses only 1 complete square region (that is in the center of the figure).
⇒ There is 1 complete smallest square region enclosed by the figure.
We need to find the number of half of smallest square region enclosed by the figure.
Here, apart from the 1 complete square region, we need to see the bar which is almost half occupied by the figure.
We can say, the bar (2, 3) is almost half filled.
⇒ There is 1 half of smallest square region enclosed by the figure.
We need to find the number of more than half of smallest square region enclosed by the figure.
Here, apart from the 1 complete square region and 1 half of square region, we can see that 6 bars looks like more than half of smallest square regions.
⇒ There are 6 more than half of smallest square region enclosed by the figure.
We need to find the number of less than half of smallest square region enclosed by the figure.
Here, apart from the 1 complete square region, 1 half of square region and 6 more than half of square regions, we can see that only 1 bar seems to look like less than half of square region.
⇒ There is 1 less than half of smallest square region enclosed by the figure.
Now, we need to find the total area of the figure, given that area of one smallest square region is 1 cm2.
To find area of the figure:
The figure consists of a central circle and four semi-circular petals surrounding it.
The radius of the central circle can be out as:
Draw a straight line from the mid of the circle and measure the line, comes out to be 1.4 cm (approx.).
Since, the line covers one complete bar and 2/5th part of another bar.
So, length of one complete bar = 1 cm
And, ![]()
![]()
![]()
![]()
This length is actually the diameter of the central circle.
If ![]() , then
, then
![]()
![]()
Area of circle is given by
Area = πr2
![]()
![]()
⇒ Area = 1.54 cm2 …(i)
The four surrounded petals are semi-circular. So, joining any two petals would make a circle. We have 2 circles.
Radius of these circle = 1 cm
As the petals approximately covers one complete bar.
So,
Area of one circle of radius 1 cm is given by,
![]()
![]()
⇒ Area = 3.14 cm2
So, area of 2 similar circles = 2 × 3.14 cm2
⇒ Area of 2 circles = 6.28 cm2 …(ii)
Adding (i) and (ii) to get area of the whole figure, we have
Area of whole figure = 1.54 + 6.28
⇒ Area of whole figure = 7.82 cm2
Hence, we have taken out the data of shape 6.
For shape 7:
Let us name the figure as ABCDEFGHIJKLMNOP.
We need to find number of complete smallest square regions enclosed by the figure.
We have drawn the figure roughly.
Note, the central bar is complete and is enclosed by the figure.
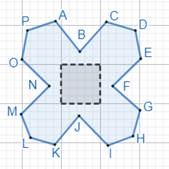
⇒ There is 1 complete smallest square region enclosed by the figure.
We need to find number of half of smallest regions enclosed by the figure.
Apart from the 1 complete square region, we can see that there are 4 regions that can be considered as half of square region.
⇒ There are 4 half of smallest square regions enclosed by the figure.
We need to find number of more than half of smallest regions enclosed by the figure.
Apart from 1 complete square region and 4 half of square region, we can see that there are 4 more than half of square region.
⇒ There are 4 more than half of square regions enclosed by the figure.
We need to find number of less than half of smallest regions enclosed by the figure.
Apart from 1 complete square region, 4 half of square regions and 4 more than half of square regions, we can see no other region less than half of square region.
⇒ There are 0 less than half of square region enclosed by the figure.
Now, we need to find the total area of the figure, given that area of one smallest square region is 1 cm2.
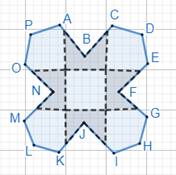
To find area of the figure:
Dissipate the figure into smaller general shapes.
It can be broken down to several squares and triangles for ease of calculation.
Take BNJF as a square, since it is approximately a square.
BNJF seems to be one completely bar approximately, and we know area of a complete bar = 1 cm2
So, Area of BNJF = 1 cm2 …(i)
Take ABNO, CBFE, FGIJ and JKMN as squares with same dimensions.
So, Area of ABNO = Area of CBFE = Area of FGIJ = Area of JKMN = 1 cm2 …(ii)
[∵, they are approximately equal to a complete bar]
Take ∆OPA, ∆CDE, ∆GHI and ∆KLM as triangles with same dimensions (as they are approximately).
Let us take out are of ∆OPA.
Base = OA = 1 cm [∵, BN = OA = 1 cm]
![]() [taken approximately]
[taken approximately]
Area is given by,
![]()
![]()
![]()
So,
![]() …(iii)
…(iii)
Add all the area to get a total area of the figure.
Adding (i), (ii) & (iii), we get
![]()
![]()
![]()
![]()
⇒ Total Area = 5.8 cm2
Hence, we have taken out the data of shape 7.
For shape 8:
We have from the question:

Since, the shape given is not of uniform nature, we shall find the answer to approximations.
We need to find the number of complete smallest square region enclosed by the figure.
Here, either we can draw the figure by hand on a graph paper, or we need to imagine the bar lines which are missing behind the rigid figure.
Clearly, the figure encloses 2 complete square regions.
⇒ There are 2 complete smallest square regions enclosed by the figure.
We need to find the number of half of smallest square region enclosed by the figure.
Apart from the 2 complete square regions, we can see that there are 4 regions that covers approximately half of square regions.
⇒ There are 4 half smallest square regions enclosed by the figure.
We need to find the number of more than half of smallest square regions enclosed by the figure.
Apart from 2 complete square regions and 3 half of square regions, we can see that there are 5 regions which can be said that they are covering more than half of smallest square regions.
⇒ There are 5 more than half of smallest square regions enclosed by the figure.
We need to find the number of less than half of smallest square regions enclosed by the figure.
Apart from 2 complete square regions, 3 half of square regions and 5 more than half of square regions, we can see that there are 8 regions which are approximately less than half of square regions.
⇒ There are 7 less than half of smallest square regions enclosed by the figure.
Now, we need to find the total area of the figure, given that area of one smallest square region is 1 cm2.
To find area of this disfigured shape:
We need to merge halves together to form one complete bar.
We need to merge more than halves and less than halves together to form one complete bar.
Finding area by this way only leads us to an approximate area.
Data:
Complete bars = 2
⇒ Area of 2 complete bars = 2 cm2 [∵, Area of 1 complete bar = 1 cm2] …(i)
Half bars = 4
And by merging 2 half bars, we get 1 complete bar.
So, by merging 4 half bars, we get 2 complete bars.
⇒ Area of 2 complete bars = 2 cm2 …(ii)
More than half bars = 5
Less than half bars = 7
And by merging 1 more than half bar and 1 less than half bar, we get 1 complete bar.
So, by merging 5 more than half bars and 5 less than half bars, we get 5 complete bars.
⇒ Area of 5 complete bars = 5 cm2 …(iii)
Now, we are left with 2 less than half bars, which can be merged to make a half bar.
If area of 1 complete bar = 1 cm2
Then,
![]()
⇒ Area of 1 half bar = 0.5 cm2 …(iv)
Adding all these areas, we get
Area of the figure = 2 + 2 + 5 + 0.5 [∵, from (i), (ii), (iii) & (iv)]
⇒ Area of the figure = 9.5 cm2
Hence, we have taken out the data of shape 8.
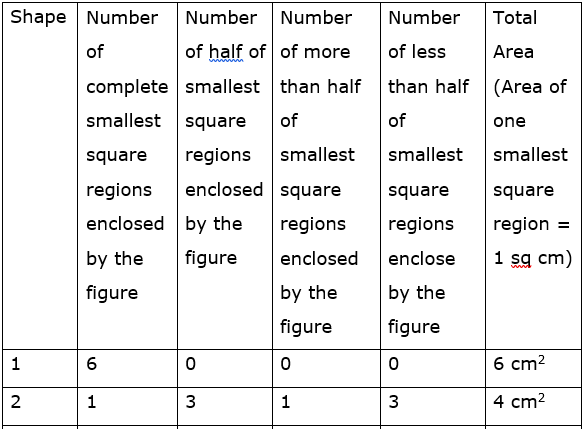
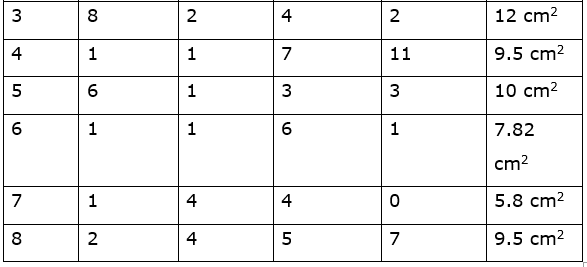
Filling the derived data of shape 1, 2, 3, 4, 5, 6, 7 and 8 in the table, we get