Figure shows a vessel partitioned by a fixed diathermic separator. Different ideal gases are filled in the two parts. The rms speed of the molecules in the left part equals the mean speed of the molecules in the right part. Calculate the ratio of the mass of a molecule in the left part to the mass of a molecule in the right part.

In kinetic theory of ideal gas, the average energy is given by

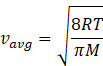
Where R=gas constant=8.31Jmol^-1K^-1

T=temperature of gas

M=molar mass of gas

We know that,

Gas constant R=k_BN_A

Where k_B= Boltzmann constant = 1.38 × 10^–23 J K^–1.

N_A=Avogadro number=6.02310^-23 mol^-1

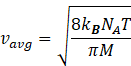
Molar mass of gas molecule M= Avogadro numbermass of gas molecule

M=N_Am

So average velocity becomes

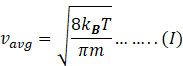
Rms speed of gas molecule is given by

Where R=gas constant 8.31J/molK

T=temperature of gas

M=molar mass of gas

Putting the value gas constant R=k_BN_A

So rms speed becomes

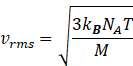
M=N_Am

Therefore,

Let the mass of molecule in left part=m₁

Mass of molecule in right part=m₂

According to question, the rms speed of the molecules in the left part equals the mean speed of the molecules in the right part.

So, from equation (I) and(II) we get

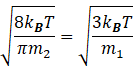
Since the walls of separator is diathermic therefore temperature of both the parts will be same.

Squaring the above equation, we get

The ratio of the mass of a molecule in the left part to the mass of a molecule in the right part is 1.17.