A vessel of volume V0 contains an ideal gas at pressure p0 and temperature T. Gas is continuously pumped out of this vessel at a constant volume-rate dV/dt = r keeping the temperature constant. The pressure of the gas being taken out equals the pressure inside the vessel. Find (a) the pressure of the gas as a function of time, (b) the time taken before half the original gas is pumped out.
Let P be the pressure and n be the number of moles of gas inside the vessel at any given time.
As mentioned in question, pressure is decreasing continuously. So, suppose a small amount of gas ‘dn’ moles are pumped out and the decrease in pressure is ‘dP’.
So, pressure of remaining gas =P-dP
Number of moles of remaining gas =n-dn
Given
The volume of gas =Vo
Temperature of gas=T
We know that ideal gas equation
PV=nRT
Where V= volume of gas
R=gas constant =8.3JK-1mol-1
T=temperature
n=number of moles of gas
P=pressure of gas.
So, applying ideal gas equation for the remaining gas
(P-dP) Vo=(n-dn) RT
P
Vo-dP
Vo=n
RT-dn
RT …… (1)
Applying ideal gas equation, before gas was taken out
PVo = nRT ……. (2)
Using equation (2) in (1) we get
n
RT - Vo
dP = n
RT - dn
RT
Vo
dP=dn
RT …… (3)
According to question, pressure of gas being taken out is equal to inner pressure of gas always. So inner pressure is equal to P-dP
Let the volume of gas taken out dV.
Applying ideal gas equation to gas pumped out
(P-dP) dV=dn
RT
PdV=dn
RT …… (4)
Where we have ignored dPdV as it is very small and can be neglected.
From equation (3) and (4)
Vo
dP=P
dV
Given 
. Since volume is decreasing so rate should be negative.
Putting this value of dV in equation (5)
(a) Integrating equation (6) from Po to P and t=0 to t
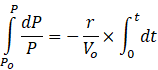
Where we have used the formula
And
Taking exponential on both sides,
The pressure of the gas as a function of time is given as 
(b) In second part the final pressure becomes half of the initial pressure
Putting this value of P in equation (7)
Taking natural logarithm on both side
The time taken before half the original gas is pumped out is 