A bar magnet of length 1 cm and cross-sectional area 1.0 cm² produces a magnetic field of 1.5 × 10^–4 T at a point in end-on position at a distance 15 cm away from the centre.

(a) Find the magnetic moment M of the magnet.

(b) Find the magnetization I of the magnet.

(c) Find the magnetic field B at the centre of the magnet.

Given:

Length of bar magnet=1cm=10^-2m

Cross section area of magnet=1.0cm² =10^-4m²

Magnetic field at a point in end on position =1.5× 10^-4T

Distance of point from centre=15cm=15× 10^-2m

We need to find the magnetic field at a point in the axis of magnet

Which is given by

Where

M=magnetic moment of the magnet

d=distance of point from centre of magnet

l=half the length of magnet

Proof:

Suppose SN is magnet of length 2l and pole strength m

We need to find the magnetic field at a point P which lies on the axis of magnet at a distance d from the centre.

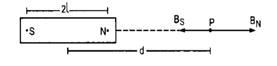
The magnetic field at P due to north pole of the magnet B_N

And it is in rightward direction

Similarly magnetic field at P due to south pole of magnet is given by

Which is in leftward direction(-ve)

The net magnetic field is then given by

Now magnetic moment of magnet is given by

…..(i)

Where

m=pole strength

l=length of magnet

using eqn.(i) we get

Putting the values of l ,d, B and μ₀ we get

Solving the equation we get

Therefore magnetic moment M of the magnet is 2.5Am²

Intensity of magnetization(I) is given by formula

Volume of bar magnet =

Where

A=cross-section area of magnet

l=length of bar magnet

hence we get

Putting the values of M, A and l

We get

Therefore magnetization intensity is 2.5× 10⁶A/m

we know that magnetic field at a point P due to a magnetic charge m at a distance d from it is given by

Using eqn.(i) we get

….(ii)

Also magnetizing intensity H is given by formula

Using eqn.(ii) we get

The total magnetic field intensity at the centre of magnet due to magnet is equal to sum of magnetic field intensities due to north pole(H_N) and south pole (H_s)

Magnetic field intensity due to north and south pole are equal in magnitude (by symmetry)

∴

Putting the values of M,d and l

We get

Now net magnetic at the centre B is given by

Where

μ_o=permeability of the free space

H=magnetic field intensity

I=intensity of magnetization

Putting the value of H and I we get

Therefore, magnetic field B at the centre of the magnet is 3.14T