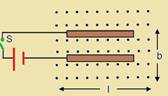
Two metal strips, each of length ℓ, are clamped parallel to each other on a horizontal floor with a separation b between them, A wire of mass m lies on them perpendicularly as shown in figure. A vertically upward magnetic field of strength B exists in the space. The metal strips are smooth but the coefficient of friction between the wire and the floor is μ. A current i is established when the switch S is closed at the instant t = 0. Discuss the motion of the wire after the switch is closed. How far away from the strips will the wire reach?

Given-

Length of the two metallic strips = l

Distance between the strips = b

Mass of the wire = m

Strength magnetic field = B

Coefficient of friction between the wire and the floor = μ

Let the wire moved by a distance x.

The magnetic field present,will act on the wire towards the right.

As coefficient of friction is zero as the space between the wire and strip is smooth .

Due to the influence of magnetic force, the wire firstly will travel a distance equal to the length of the strips.

After this, it travels a distance x and then ,a frictional force will act opposite to its direction of motion on the wire.

So work done by the magnetic force and the frictional

force will be equal.

where

μ is the coefficient of friction for the two surfaces

W is the weight of the object

= mass × acceleration due to gravity

= mg

Magnetic force due to presence of current given by –

where,

B= magnetic field

I = current

l = length of the wire

and θ = the angle between B and l

Thus,