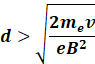An electron is emitted with negligible speed from the negative plate of a parallel plate capacitor charged to a potential difference V. The separation between the plates is d and a magnetic field B exists in the space as shown in figure. Show that the electron will fail to strike the upper plate if.

Given-
Potential difference applied across the plates of the capacitor = V
Separation between the plates = d
Magnetic field intensity = B
The electric field applied across the plates of a capacitor
,
![]()
Also, coulomb’s force experienced by the electron is given by,
![]()
where e= charge on the electron and
E= electric field applied
Hence, the force experienced by the electron due to this electric field,
![]()
Now, acceleration a is given by-
![]()
![]()
where
e = charge of the electron
me = mass of the electron
From 3rd equation for motion
![]()
where
u = initial velocity
v= final velocity
s=distance travelled
and a = acceleration of the particle
substituting the value of a-
![]()
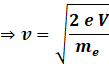
The electron will move in a circular path due to the presence of the magnetic field.
The radius of the circular path described by a particle in a magnetic field r,
![]()
where,
m is the mass of a proton
v= velocity of the particle
B = magnetic force
q= charge on the particle =![]() C
C
Radius of the circular path followed by the electron is ,
![]()
And the electron will fail to strike the upper plate of the
capacitor if and only if the radius of the circular path will be less
than d,
i.e. d>r
![]()
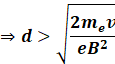
Thus, the electron will fail to strike the upper plate if