A circular disc made of iron is rotated about its axis at a constant velocity ω. Calculate the percentage change in the linear speed of a particle of the rim as the disc is slowly heated from 20°C to 50°C keeping the angular velocity constant. Coefficient of linear expansion of iron = 1.2 × 10^–3 °C^–1.

Question

A circular disc made of iron is rotated about its axis at a constant velocity ω. Calculate the percentage change in the linear speed of a particle of the rim as the disc is slowly heated from 20°C to 50°C keeping the angular velocity constant. Coefficient of linear expansion of iron = 1.2 × 10^–3 °C^–1.

Philoid · Accepted Answer

Given:
T₁ = 20 ° C
T₂ = 50 ° C
Δ T = 50-20= 30° C
Angular Velocity: ω = constant
Coefficient of linear expansion of iron : α = 1.2 × 10^–5 °C^–1.
Formula used:
We know that:

Here, v is the velocity of the particle and r is the radius of the particle.
When temperature is increased from 20° C to 50° C, the disc undergoes thermal expansion.
Let r be the radius of particle at T₁and r’ be the changed radius of particle at T₂_.Let v be the velocity of particle at T₁ and v’ be the velocity of particle at T₂_.
Hence,
Angular Velocity at T₁:
Angular Velocity at T₂ :
Now, we know that Thermal linear expansion of radius is:
Angular velocity is constant even after heating the disc,
Substituting , we get

As we know that percentage change is :

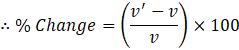
Hence the percentage change in the linear speed of a particle of the rim when the disc is slowly heated from 20°C to 50°C keeping the angular velocity constant is 0.036%.