Consider the situation shown in figure. The frame is made of the same material and has a uniform cross-sectional are everywhere. Calculate the amount of heat flowing per second through a cross-section of the bent part if the total heat taken out per second from the end at 100°C is 130J.

For the above frame, redrawing the fig,

(1)

The equivalent resistance network becomes –

Let R_AB, R_BC, R_CD, R_DE, R_{EF and} R_BE be the equivalent resistance across each cross-section as shown in fig. below –

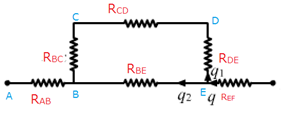
(2)

Resistance in terms of conductivity

R= (1)

From fig (1) and (2)and equation (1)

R_{AB = ,} R_{BC = ,} R_{CD =,} R_{DE =,} R_EF= and R_{BE =}

Now, lets reduce the network into equivalent network .

Since R_BC R_CD R_DE are connected in series, let R₁ be their equivalent resistance.

Then R_{1 =} R_BC+R_CD + R_DE

₌

=

Now the circuit reduces to –

Now from Kirchhoff’s current law(KCL), we know The algebraic sum of all currents entering and exiting a node must equal zero

Hence ,KCL at point E , since -

q = q₁ +q₂

Now, since R₁ and R_BE are in parallel, so total heat across R1 and R_BE will be same.

ie, q₁R₁ = q₂R_BE

⇒ =

⇒ q₂ =

Now, q = q₁ +q₂

= q₁ + q₁

Given q = 130 J, substituting above

130 =

⇒ q₁ = 60 J