The three rods shown in figure have identical geometrical dimensions. Heat flows from the hot end at a rate of 40 W in the arrangement

(a) Find the rates of heat flow when the rods are joined as in arrangement (b) and in (c). Thermal conductivities of alumimium and copper are 200 W m^–1 °C^–1 and 400 W m^–1 °C^–1 respectively.

(a).Let’s redraw the diagram

Since all rods are connected in series,

R_eq = R_Al + R_Cu + R_Al

Given -

Temperature of the hot end ,T₁ = 100°C

cold end ,T₂ = 0°C

Substitution for R_eq –

R_eq =

Given Thermal conductivities of aluminium =200 W m–1 °C–1

Copper = 400 W m–1 °C–1

Therefore

R_eq = + + ) =

Now rate of flow of heat,

=

= (1)

Given rate of flow of heat

From (1)

40 = 80 × 100 ×

⇒ (2)

(b) Lets redraw the diagram –

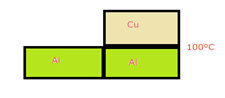
The equivalent circuit in terms of thermal resistances becomes-

R_eq = R_Al +

= ++

=

=

Now rate of flow of heat,

=

= (3)

From (2)

Substituting in (3)

=

= 75 W

(c) Lets redraw the diagram-

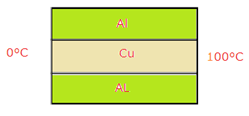
Since the thermal resistors are connected in parallel.

= + +

⇒ =

⇒ = (_Al + _Al +_Cu ) = (200+200+400)

⇒ = *(800)

⇒ =

From (2)

⇒ =

⇒ = 400W