A hollow metallic sphere of radius 20 cm surrounds a concentric metallic sphere of radius 5 cm. The space between the two spheres in filled with a nonmetallic material. The inner and outer spheres are maintained at 50°C and 10°C respectively and it is found that 100 J of heat passes from the inner sphere to the outer sphere per second. Find the thermal conductivity of the material between the spheres.

Let’s redraw the circuit –

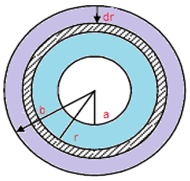
Let-
Radius of the inner sphere =a
Radius of the outer sphere = b

Given –

a = r₁ = 5cm = 0.05m

b = r₂ = 20cm = 0.2m

θ₁ = T₁ = 50°C

θ₂ = T₂ = 10°

Consider an imaginary shell of radii r and thickness dr.

Area,

Now, rate of flow of heat –

=-

= is change in temperature.

A= Area of cross section of the tube

K = thermal conductivity of the tube

d_r = change in length

Here, the negative sign is for decrease in temperature with increase in radius.

q = -

Taking integral on both sides –

=

Solving above integral –

q= = k( ) = 100 (given)

Substituting the values,

K = = 2.8 = 3 W m-1°C-1