A metal sphere of radius R is charged to a potential V.

a) Find the electrostatic energy stored in the electric field within a concentric sphere of radius 2R.

b) Show that the electrostatic field energy stored outside the sphere of radius 2R equals that stored within it.

J

Explanation:

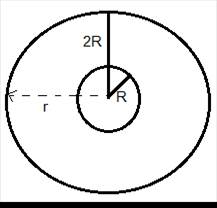
The given condition is represented in the figure. The outer sphere has a radius 2R while the metal sphere has a radius R.

Now potential difference, V of the sphere is given by,

Where Q and C represents Charge and Capacitance of sphere

For sphere of radius R, C is

Substituting this in eqn.1, we get,

a)

Energy density at a distance r from the centre is,

Or

Consider a spherical element at a distance r from the centre, with a thickness dr, such that R>r>2R.

Now the volume of the spherical element is,

So, energy stored will be

Or

For finding the electrostatic energy on a surface at 2R, we have to integrate the expression for dU_E in between R and 2R. So,

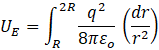
Or,

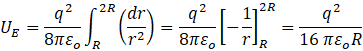
But from eqn.2,

Hence, U_E becomes,

Or,

Electrical energy at a distance 2R is

b)

To find the electrostatic stored energy outside the radius 2R, we integrate the above expression for differential of stored energy from 2R to infinity.

So,

Or,

By substituting q as 4πε₀×R×V in the above expression, we get,

Or it will reduce to,

This is same as that of inside the sphere of radius 2R.

Thus electrostatic field energy stored outside the sphere of radius 2R equals that stored within it.